Prime numbers

Prime numbers are fascinating mathematical objects that have intrigued mathematicians for centuries. In this blog, we will explore the properties and patterns of prime numbers and discuss why they are so important in mathematics.

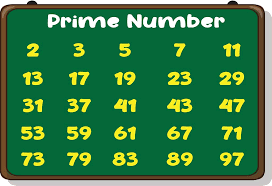
First, let’s define what a prime number is. A prime number is a positive integer greater than 1 that has no positive integer divisors other than 1 and itself. For example, the first few prime numbers are 2, 3, 5, 7, 11, and 13.

One of the most interesting properties of prime numbers is that they are the building blocks of all positive integers. Every positive integer can be expressed as a unique product of prime numbers. This fact is known as the fundamental theorem of arithmetic.

Prime numbers also exhibit several interesting patterns. For example, prime numbers are only found in certain positions in the sequence of positive integers. Specifically, they are found at every other position starting with 2 (i.e., 2, 3, 5, 7, 11, 13, 17, etc.). This is known as the prime number theorem.

There are also many unsolved problems related to prime numbers. One of the most famous of these is the Riemann hypothesis, which seeks to provide a formula for the distribution of prime numbers. Despite intense efforts by mathematicians over the past century, the Riemann hypothesis remains unsolved.

Prime numbers are also important in computer science and cryptography. They are used extensively in the RSA encryption algorithm, which is widely used to secure online communications and financial transactions.

In conclusion, prime numbers are fascinating objects that have captivated mathematicians for centuries. They play a fundamental role in number theory and have important applications in computer science and cryptography. While much is known about prime numbers, there is still much more to be discovered about these intriguing mathematical objects.

Do this quiz to see your knowledge of prime numbers!

[ays_quiz id=’5′]